타원 곡선 암호: Difference between revisions
From CS Wiki
No edit summary |
No edit summary |
||
| Line 7: | Line 7: | ||
** 160비트의 ECC가 1024비트의 RSA와 동일한 보안수준 | ** 160비트의 ECC가 1024비트의 RSA와 동일한 보안수준 | ||
** 키 생성 시간이 RSA에 비해 수십배 이상 빠름 | ** 키 생성 시간이 RSA에 비해 수십배 이상 빠름 | ||
== 키 생성 과정 == | |||
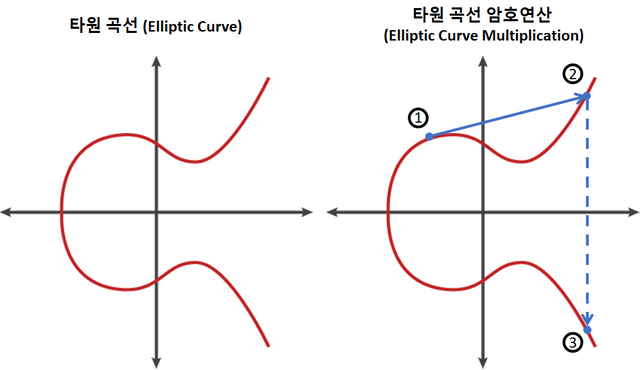
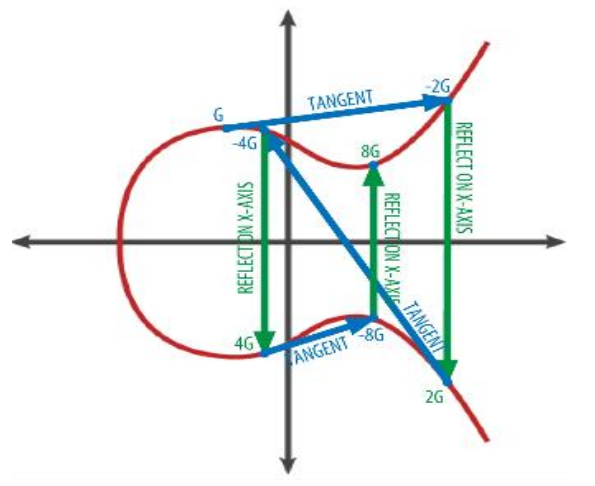
; 곡선의 수식: y<sup>2</sup> = x<sup>3</sup> + ax + b | |||
[[파일:타원 곡선 암호 연산.png|x250px]][[파일:타원 곡선 암호 연산2.png|x250px]] | |||
* ① 생성 포인트 시작해서 타원곡선의 접선을 그음 | |||
* ② 타원곡선과 만나는 점을 찍음 | |||
* ③ ②번에서의 점과 대칭인 점이 목표점 | |||
* 위의 과정은 반복하기 쉬우나, ③번 목표점 ①번의 생성점을 찾긴 매우 어려움 | |||
== [[RSA]]와 [[ECC]]의 비교 == | == [[RSA]]와 [[ECC]]의 비교 == | ||
| Line 35: | Line 43: | ||
| 오랜 기간 입증된 안전성 | | 오랜 기간 입증된 안전성 | ||
|} | |} | ||
== 사용 시 주의사항 == | |||
== 같이 보기 == | == 같이 보기 == | ||
* [[RSA]] | * [[RSA]] | ||
== 참고 문헌 == | |||
* [https://steemit.com/dclick/@eaglekeeneye/-5-bitcoin-2-1544235909120 Bitcoin은 어떻게 신뢰를 얻게 되었나 2 | |||
] | |||
Revision as of 07:08, 19 January 2020
- ECC, Elliptic Curve Cryptosystem
- RSA의 대안으로 대두된 이산대수의 난해성에 기반한 공개키 암호화 알고리즘
- 창시자 : 코블리츠(N.Koblitz), 밀러(V.S.Miller)
- RSA보다 키의 비트수를 적게 하면서 동일한 성능을 제공
- 160비트의 ECC가 1024비트의 RSA와 동일한 보안수준
- 키 생성 시간이 RSA에 비해 수십배 이상 빠름
키 생성 과정
- 곡선의 수식
- y2 = x3 + ax + b
- ① 생성 포인트 시작해서 타원곡선의 접선을 그음
- ② 타원곡선과 만나는 점을 찍음
- ③ ②번에서의 점과 대칭인 점이 목표점
- 위의 과정은 반복하기 쉬우나, ③번 목표점 ①번의 생성점을 찾긴 매우 어려움
RSA와 ECC의 비교
| 구분 | ECC | RSA |
|---|---|---|
| 속도 | 빠름 | 느림 |
| 키 길이 | 짧음 | 김 |
| 시장점유율 | 낮음 | 높음 |
| 주요 사용처 | 모바일 환경
(그 외 환경으로 확대 중) |
유선 환경 |
| 장점 | 효율성 | 오랜 기간 입증된 안전성 |
사용 시 주의사항
같이 보기
참고 문헌
- [https://steemit.com/dclick/@eaglekeeneye/-5-bitcoin-2-1544235909120 Bitcoin은 어떻게 신뢰를 얻게 되었나 2
]