의사결정 나무

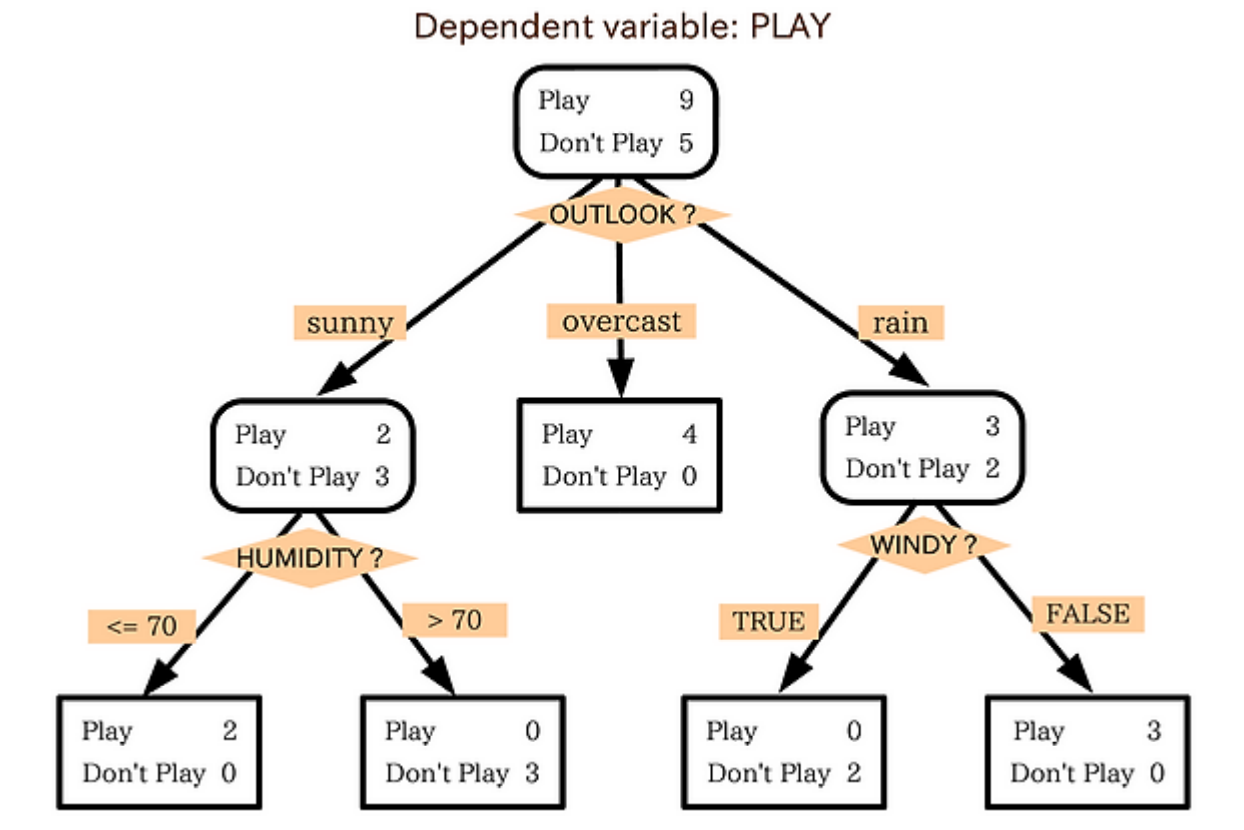
Decision Tree

의사결정 규칙을 나무 구조(Tree)로 도표화하여 분류와 예측을 수행하는 분석 방법

• 데이터들의 속성을 기반으로 분할 기준을 판결하고, 분할 기준에 따라 트리 형태로 분기하여 모델링
• 데이터 분석 결과가 의사결정 나무의 분기점을 통해 시각적으로 확인할 수 있어 해석이 용이

과정

단계	설명
의사결정 나무 형성	분석 목적과 자료구조에 따라 적절하게 분리 규칙, 분리 기준 및 정지 규칙 지정
가지치기	분류오류(Classification Error) 유발 위험이 높거나 부적절한 규칙을 가지는 가지(Branch) 제거
타당성 평가	이익, 비용, 위험 등을 고려하여 모형을 평가하는 단계
해석 및 예측	해석 결과에 따라 분류 및 예측 모형 설정

의사결정 나무 형성

• 분리 규칙(Splitting Rule)
• 분리 기준(Splitting Criterion)
  • 이산형 목표 변수: 카이제곱 통계량의 p-값, 지니 지수, 엔트로피 지수 등
  • 연속형 목표 변수: 분산 분석의 F-통계량, 분산의 감소량
• 정지 규칙(Stopping Rule): 더 이상 분기 되지 않고 끝마디가 되도록 하는 규칙

가지치기

• 에러 감소 가지치기(Reduced Error Pruning): 오류가 더 이상 줄어들지 않을 때 까지 반복
• 룰 포스트 가지치기(Rule Post Pruning): 정확도가 낮은 순서대로 제거
  • 과적합 문제 방지를 위해 사전(pre-pruning) 가지치기, 사후(post-pruning) 가지치기 수행

타당성 평가

• 이익 도표(Gains Chart)
• 위험 도표(Risk Chart)
• 검정 자료(Test Data)
• 교차 검증(Cross Validation)

구성요소

구성요소	설명
뿌리 마디(Root Node)	나무가 시작되는 마디로 전체 자료를 포함
중간 마디(InternalNode)	부모와 자식 마디를 모두 가진 마디
끝 마디(Terminal Node)	자식 노드가 없는 마디
부모 마디(Parent Node)	주어진 노드의 상위 마디
자식 마디(Child Node)	주어진 노드의 하위 마디
가지(Branch)	하나의 마디로부터 끝 마디까지 연결된 마디들
깊이(Depth)	가지를 이루는 마디의 개수

활용 알고리즘

알고리즘	설명
CHAID	카이제곱 검정(범주형 목표변수) 또는 F-검정(연속형 목표변수)을 이용하여 다지분리(Multiway Split) 수행
CART	지니 지수(Gini Index, 범주형) 또는 분산의 감소량(연속형)을 이용하여 이진분리(Binary Split) 수행
CS5.0	명목형 목표 변수를 지원하는 가장 정확한 알고리즘으로, 다지분리(범주)및 이진분리(수치) 수행
랜덤 포레스트	부트스트래핑(Bootstrapping), 배깅(Bagging) 등의 앙상블(Ensemble) 기법을 활용

장단점

• 장점
  • 이해하기 쉬운 모델 형태
  • 여러 변수의 영향도 파악 용이
  • 계산복잡성 대비 높은 예측 성능
  • 분류(classification)와 회귀(regression) 모두 가능

→ 범주나 연속형 수치 모두 예측

• 단점
  • 최적해를 보장하지 못함(Greedy 알고리즘)
  • 비연속성 분류
  • 결정경계(decision boundary)가 데이터 축에 수직인 데이터에만 최적화