Logistic regression: Difference between revisions
From CS Wiki
(로지스틱 회귀에 대한 넘겨주기를 제거함) Tags: Removed redirect Visual edit |
No edit summary |
||
| Line 1: | Line 1: | ||
{{DISPLAYTITLE:로지스틱 회귀}} | {{DISPLAYTITLE:로지스틱 회귀}} | ||
Logistic regression is a statistical and machine learning technique widely used to solve binary classification problems. This algorithm predicts the probability that the outcome variable (dependent variable) belongs to a specific class through a linear combination of independent variables. Although it is primarily applied in binary classification with labels of 0 or 1, it can be extended to multiclass classification as well. | '''Logistic regression is a statistical and machine learning technique widely used to solve binary classification problems.''' This algorithm predicts the probability that the outcome variable (dependent variable) belongs to a specific class through a linear combination of independent variables. Although it is primarily applied in binary classification with labels of 0 or 1, it can be extended to multiclass classification as well. | ||
* '''Logistic''': Used in scenarios requiring dichotomous outcomes, such as pass/fail, success/failure, survival/death, or true/false. | * '''Logistic''': Used in scenarios requiring dichotomous outcomes, such as pass/fail, success/failure, survival/death, or true/false. | ||
| Line 30: | Line 30: | ||
*[[회귀 분석|Regression Analysis]] | *[[회귀 분석|Regression Analysis]] | ||
*[[선형 회귀|Linear Regression]] | *[[선형 회귀|Linear Regression]] | ||
[[분류:Data Science]] | |||
Revision as of 21:55, 30 October 2024
Logistic regression is a statistical and machine learning technique widely used to solve binary classification problems. This algorithm predicts the probability that the outcome variable (dependent variable) belongs to a specific class through a linear combination of independent variables. Although it is primarily applied in binary classification with labels of 0 or 1, it can be extended to multiclass classification as well.
- Logistic: Used in scenarios requiring dichotomous outcomes, such as pass/fail, success/failure, survival/death, or true/false.
- Regression analysis: Predicts future outcomes based on past trends. Since logistic regression analysis has a categorical dependent variable, it is closer to a classification model.
Functions Used
| Function | Formula |
|---|---|
| Sigmoid
1/(1+e-x) |
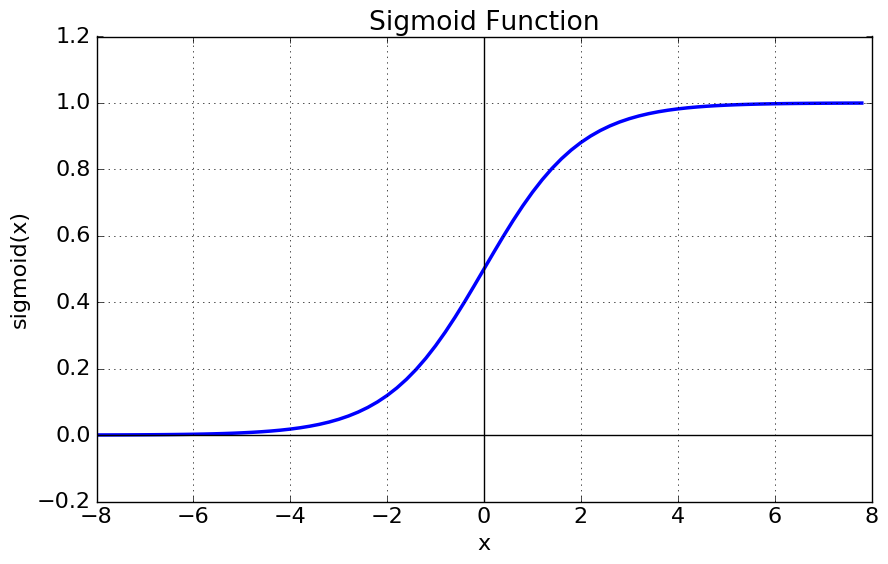
|
| 하이퍼볼릭 탄젠트
tanh(x) |
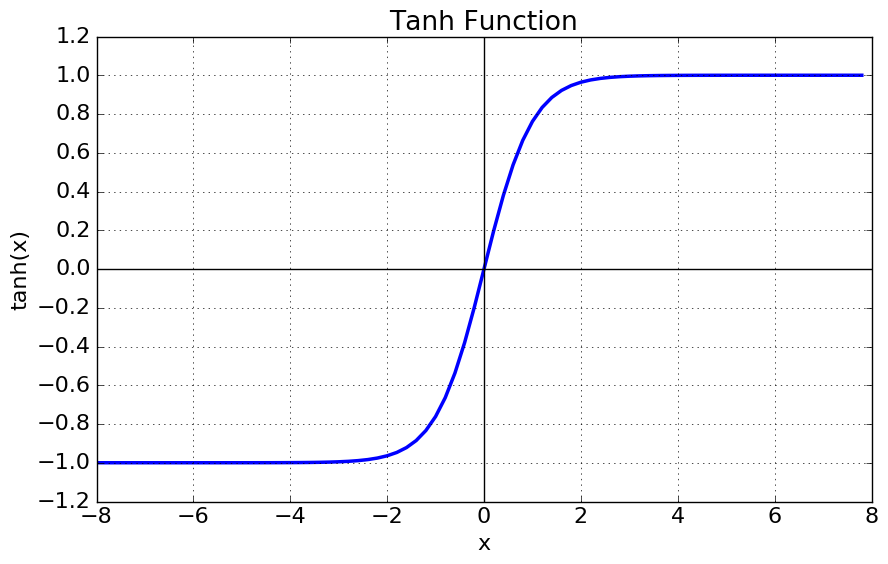
|
Types of Regression Analysis
- Simple Regression Analysis: Single independent variable
- Multiple Regression Analysis: Two or more independent variables
Advantages and Disadvantages
- Advantages: Simple to implement and easy to interpret.
- It has a relatively low risk of overfitting and is effective for binary classification.
- Disadvantages: Performs poorly with data that lacks a linear relationship.
- It is challenging to apply directly to multiclass problems, where techniques like softmax regression are often required.